如图在三角形abc中（如图三角形纸片abc中）

照此方法，我们可依次得出各三角形面积如下图所示，

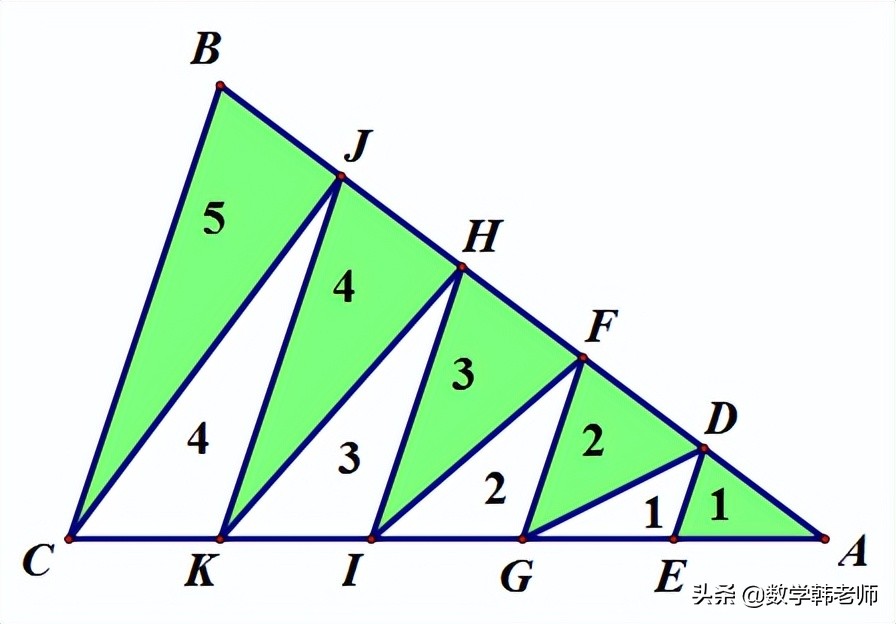
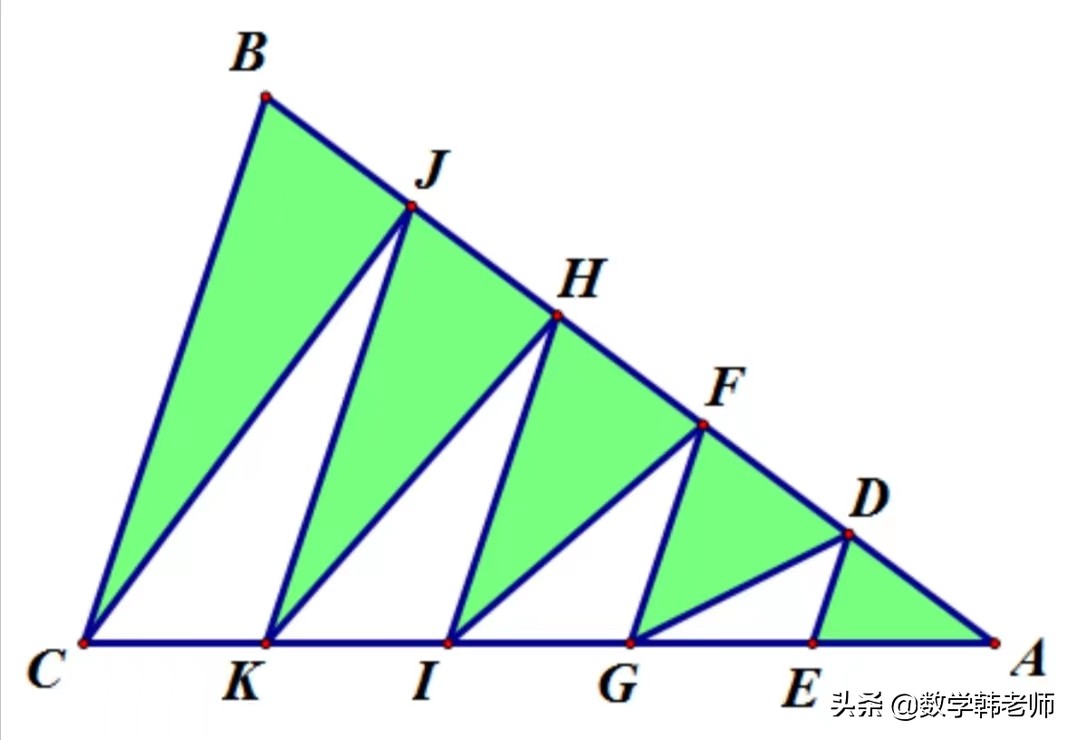
由S3与（S1+S2）等底（AD=DF）同高(点G到AF边上的高)，所以S3=S1+S2=2，

【思路解析】

等积变换在小学几何中占据重要地位，而三角形中的等积变换又非常常见，今天我们就通过一道题目来分析一下三角形中的等积变换。

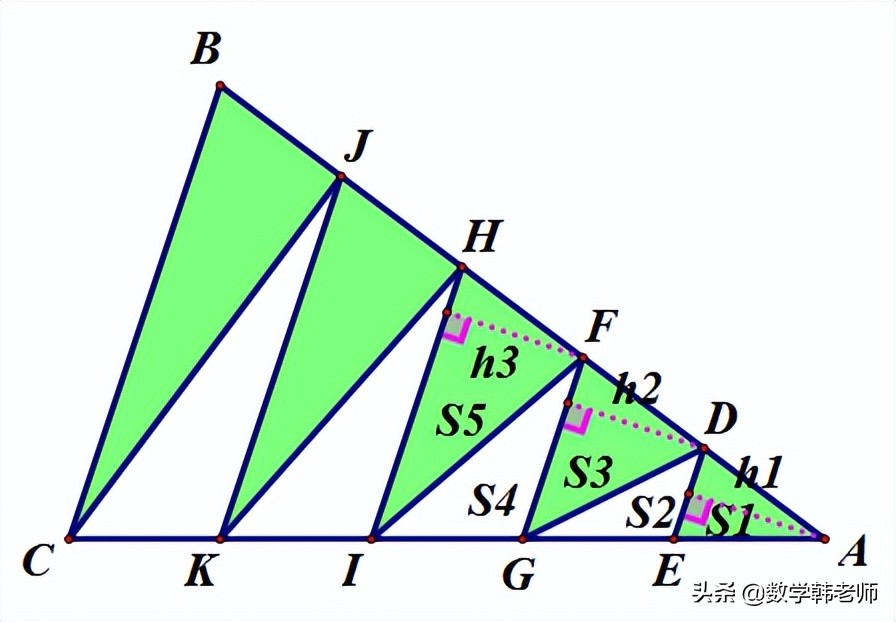
我们记这些三角形的面积分别为S1，S2，S3...,

由S5与（S1+S2+S3+S4）同高(点I到AH边上的高)底边成比例，所以面积比等于底边的比，有S5=1/2（1+1+2+2）=3，...

不足之处，请君指正。

先来看一下题目：

题目没有告诉我们具体的边长，我们如果把边长和高都设出来，用字母表示，最后能够求解，但会非常复杂。这里我们从单位面积入手，充分利用等高模型进行求解。

如下图，由于都是五等分点，所以h1=h2=h3...,

【如图，在三角形ABC中，AB、AC两边分别被五等分，则阴影部分与空白部分的面积比是______. (小学数学)】

由S2与S1同底（DE）等高（h1=h2）,所以S2=S1=1，

则阴影部分与空白部分的面积比是（1+2+3+4+5）/(1+2+3+4)=3/2.

这道题目我们就分析到这里，等积变换往往能把复杂的图形简单化，起到立竿见影的效果，我们要掌握基本模型，能融会贯通、举一反三。

我们不妨设三角形ADE的面积为单位1，即S1=1.

由S4与S3同底（FG）等高（h3=h2）,所以S4=S3=2，