等价无穷小替换公式（等价无穷小使用条件）

我们知道，谁趋近于零，谁的绝对值就越小。那么咱们怎么比较α、β趋近于零的快慢呢？用除法！只要两个数一相除，那么它们的相对大小就比较出来了，由于它们是动态的函数，只要时时刻刻满足这个规律，这个关系就不会变。另外这两个函数在某一点的极限还都是无穷小，那么由相对大小就可以比较出谁更接近于0了。

我没标注的那条线就是α的高阶无穷小

其实还有一个等价无穷小的替换，有时间咱再聊！

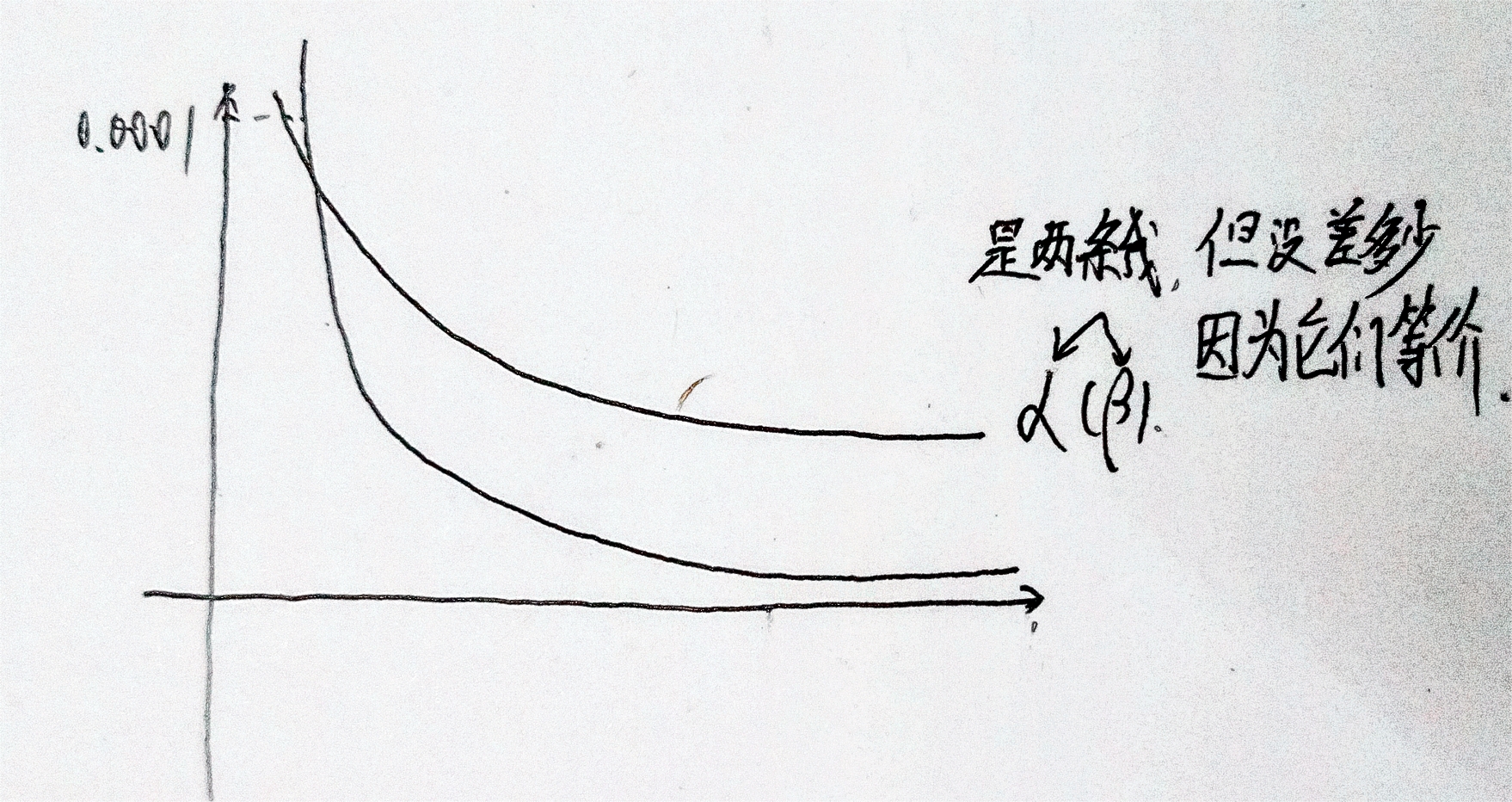
你应该明白，充要条件是可以互相推导出来的。对于这个定理你要是不理解就画一个图出来：

最后，它还有两个定理需要大家掌握：

你不要看那几条线差距大，其实这个时候，我们就应该把它看做是放大图，他们都是在趋近0.还有一个：

这个大家只要理解了第一个，剩下的就应该比较好理解。思路都是一样的。

对于一对函数而言，它们在某一点的极限可能都是无穷小，但是趋近于零的速度可能有快有慢，有的快一些有的慢一些，这也是可以比较快慢的。那么，我们要怎样比较呢？