sin90度等于多少（sin90度等于多少公式）

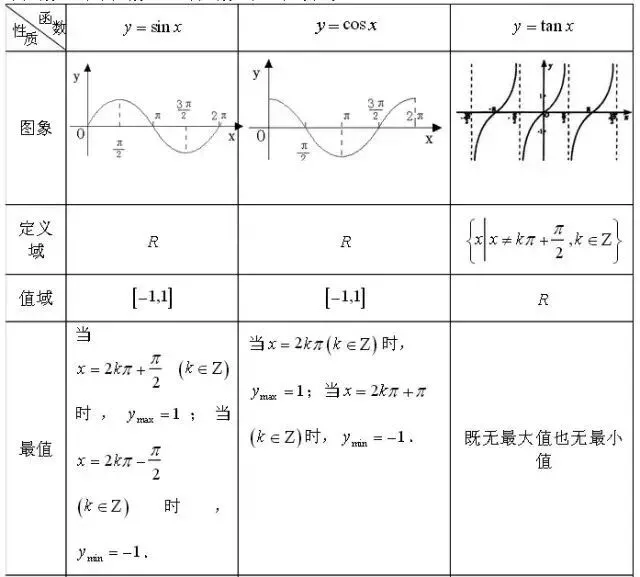
三角函数的图象性质

特殊角三角函数值

sin(α/2)=±√((1-cosα)/2)

cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ

tan(A-B) = (tanA-tanB)/(1+tanAtanB)

tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)

余割(csc)：斜边比对边，即cscA=c/a

平方关系

tanα+cotα=2/sin2α

sinα·cscα=1

secα=tanα·cscα

06

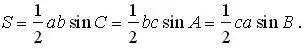
倒数关系

tan(A+B) = (tanA+tanB)/(1-tanAtanB)

万能公式

正弦(sin)：对边比斜边，即sinA=a/c

cos(A-B) = cosAcosB+sinAsinB

tan^2(α)+1=sec^2(α)

tanα-cotα=-2cot2α

cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]

tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα

tanα·cotα=1

1-cos2α=2sin^2α

积化和差公式

03

sin3A = 3sinA-4(sinA)3;

三角和的公式

锐角三角函数定义

tan(90°-α)=cotα, cot(90°-α)=tanα.

sin(90°-α)=cosα, cos(90°-α)=sinα,

正切(tan)：对边比邻边，即tanA=a/b

cos3A = 4(cosA)3 -3cosA

sin(a) = [2tan(a/2)] / {1+[tan(a/2)]2}

Cos2A = Cos^2 A--Sin2 A =2Cos2 A-1 =1-2sin^2 A

锐角三角函数公式

cot(A+B) = (cotAcotB-1)/(cotB+cotA)

余切(cot)：邻边比对边，即cotA=b/a

sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]

05

04

tanα=sinα·secα

半角公式

sin(A+B) = sinAcosB+cosAsinB

sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]

cosα=cotα·sinα

02

三角函数关系

推导公式

sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ

积的关系

cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]2}

tan2A = 2tanA/(1-tan2 A)

cscα=secα·cotα

cosα·secα=1

cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]

cot^2(α)+1=csc^2(α)

tan3a = tan a ? tan(π/3+a)? tan(π/3-a)

sinα=tanα·cosα

cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]

cos(A+B) = cosAcosB-sinAsinB

01

三角形面积定理

cos(α/2)=±√((1+cosα)/2)

1+cos2α=2cos^2α

互余角的关系

sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]

sin^2(α)+cos^2(α)=1

Sin2A=2SinA?CosA

cot(A-B) = (cotAcotB+1)/(cotB-cotA)

cotα=cosα·cscα

锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec)，余割(csc)都叫做角A的锐角三角函数。

三倍角公式

sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]

cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]

正割(sec)：斜边比邻边，即secA=c/b

和差化积公式

tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2}

两角和差公式

1+sinα=(sinα/2+cosα/2)^2

余弦(cos)：邻边比斜边，即cosA=b/c

sin(A-B) = sinAcosB-cosAsinB

倍角公式