子集和真子集的区别（子集包括真子集吗）

（10）设为全集，是的三个非空子集，且，则下面论断正确的是（ ）

7、设非空集合A={x|-2≤x≤a}, B={y|y=2x+3,x

______

例2、已知全集，且,求

A },且B∩

｝，集合B＝｛

）

，则集合

定义1：对于两个集合与，如果集合的任何一个元素都属于集合，那么集合叫作集合

的值。[来源:学科网ZXXK]

10、设集合M={x│m≤x≤m+

A}

定义2：对于两个集合A与B，如果且，那么叫做集合等于集合，记作=（读作集合等于集合

N＝{1，2，3，4，

知识点梳理：

, C={z|z= x

定义：由所有属于集合

[来源:学科网ZXXK]

的取值

A＝｛5，

1) 若A

C

x

9、集合M={（x，y）│y

（2）判定，即判定“任意，且任意”.定义3：对于两个集合与，如果，并且中至少有一个元素不属于，那么集合叫做的真子集，记作：或，读作真包含于或真包含.注2：（1）空集是任何非空集合的真子集，

}，N={x│n-

[说明]①在研究集合与集合之间关系时，这些集合往往是某个给定集合的子集，这个确定的集合就是全集。②解决某些数学问题时，有时把实数集R看作全集U，有时把有理数集Q看作全集U，有时把正整数集合看作全集U。

的补集并说明其实际意义。（课本P15习题1.3（3））

)|x、y∈R}，集合M={(x，y)|

（1）子集、真子集

的元素所组成的集合，叫做集合，记作，即根据定义可知是由集合的公共元素组成的集合，如果集合没有公共元素，则,这一条可以看成是对定义的补充，所以又有了

XK]

B．[－3，6] C．

把实数集看作是全集U，那么有理数集Q的补集CuQ就是全体无理数的集合

A．0

一、选择：

R，

三、解答

，那么“

（2）并集

,求正数

例3、设全集

R，

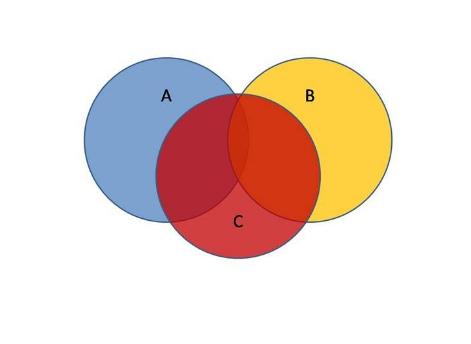
（1）U={高一（1）班的所有学生}，A={高一（1）班的女生}，B={高一（1）班的学生干部}，求A，B，

那么

B．{（2，3）} C．（2，3） D．{(x，y)|y=x+1}

8、定义差集：M－N＝{x｜ｘ

D．

A．

B=B，求a的值

，如果

(5) 已知A={0，2，4}，CuA={-1，1}，CuB={-1，0，2}，求B= 。

n 全集定义

2) 若A

[说明]A的补集是相对于全集而言的，补集的叙述要完整，必须指明是在某个全集中的补集。

=1| N={(x，y)|y≠x+1}那么M∪N的补集等于（ ）

（4）若U={1，3，a2+2a+1}，A={1，3}，CuA={5}，则a= 。

13、已知集合

，求实数

B＝｛2｝，则A

补集的性质

巩固练习

4、设集合

14、已知集合

的取值范围

R}，则M∩N=_______

} B.{x|0<x≤1} C.{x|1≤x<2} D.{x|2≤x<3} [来源:学科网ZX

（7）定义集合运算：，设，，则集合

，CuA∪CuB

合

B=B，求a的值

,x

素的个数为 （

5}，则M－（M－N）＝

3、设全集U={(x,y

（6）设、，集合，则（ ）

=

（9）已知，，若,则实数

A．充分而

A．{x|0<x<1

的取值范围。

（B）2 （C）3 （D）4

1、设集合

2、已知集合M={x|x2+14x+48<0},S={x|2a2+ax－x2<0}，若M S，则实数a∈ （ ）

n 补集定义

1，y∈

}

范围。

（11）设，对任意实数恒成立，则下列关系中成立的是（ ）

）

⑴若

，

(2) 若U={三角形}，B={锐角三角形}，则CuB= 。

的取值范围；⑵若

B＝

5、设P和Q是两个集合，定义集合

｝．若A

,

二、填空：

U），则由U中所有不属于A的元素组成的集合，叫做集合A在全集U中的补集，记作CuA，即CuA={x|x∈u，且

，若

，求正数

（3）若U={1，2，4，8}，A=?，则CuA= 。

（4）

一般地，设U为全集，A是U的一个子集（即A

）；注2：（1）如果两个集合所含的元素完全相同，那么这两个集合相等；[来源:学|科|网]

A}，读作“A补”。

R

注1：（1）有两种可能：①中所有元素是中的一部分元素；②与是中的所有元素都相同；（2）空集是任何集合的子集；任何一个集合是它本身的子集；（3）判定是的子集，即判定“任意”.

=C，则实数a的取值范围。[来源:Zxxk.Com]

6、设集合

求实数

② U=

例1、已知集合

的所有元素之和为（ ）

”的（

”是“

（1）根据交集和补集的定义容易知道，交集与并集满足交换律，即

R

_________

11、已知A={x|x2+px+q=0},B={x|x2－3x+2=0}，且A∪B=B，求p、q的关系或p、q

（1）交集

中元

或属于集合的元素所组成的集合，叫做集合与集合的并集，记为，即

，x，y∈R}，N={（x，y）│x=

1、两个集合之间的包含关系——子集、真子集与全集

，集

Ｎ}，若M＝{2，4，6，8，10

，N＝

典型例题

① U=

4、运算律

=

，

，当全集U分别取下列集合时，写出CuA。（补充）

③对任意的集合A，B，请你用集合的图示法说明是否有以上结论

Ｍ，且ｘ

① 求CuA∩CuB，Cu(A∩B)，Cu(A∪B)

，集合

例5、设U={a，b，c，d，e}，A={a，b}，B={b，c，d}，

②从上述结论中，你发现有什么结论？

① A∩CuA=φ ② A∪CuA=U ③ Cu（CuA）=A

（4）易混符号：①“”与“”②与

（2）根据子集和真子集的定义易知包含关系满足传递性，即若

，

U。

（3）交集运算满足结合律，即

（3）子集与真子集符号的方向

举例说明：解决某些数学问题时，如果

C．充分必要条件 　D．既不充分也不必要条件

例4、若集合A=

③U=

（12）已知A={x∣x+4x=0 },B={ x∣x+2(a+1)x+a-1=0}

2、两个集合的运算关系——交集、并集、补集

定义：由所有属于集合

≤x≤n}，且M，N都是集合I={x│0≤x≤1}的子集。如果把b-a称为集合{x│a≤x≤b}的“长度”，那么集合M∩N的“长度“的最小值是_____________

,

（A）1

（8）若、、为三个集合，，则一定有（ ）

课后练习

不必要条件 B．必要而不充分条件

M＝

等于（ ）

的子集，记作:或（读作：包含于或包含）

12、已知集合

（3）补集

如果一个集合含有我们所要研究的各个集合的全部元素，这个集合就可以看作一个全集，记作